mehr erfahren

Röntgen-Computertomografie

Alle innen- und außenliegenden Geometrien vollständig messen

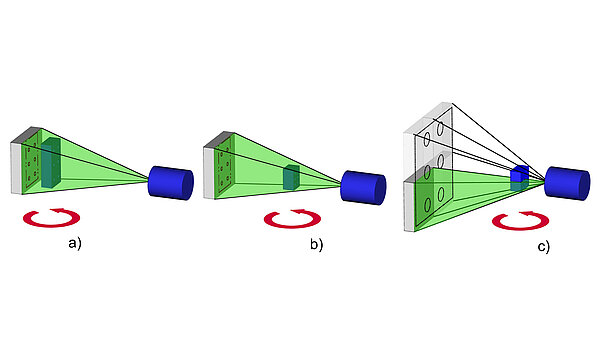
Die Röntgentomografie (auch Computertomografie, kurz CT) ermöglicht die vollständige Erfassung der Geometrie von Werkstücken unabhängig von deren Komplexität. Es werden sowohl Außen- als auch Innengeometrien erfasst. Die mangels ausreichender Genauigkeit hauptsächlich auf die Materialprüfung beschränkte industrielle Computertomografie wurde 2005 auch für die Koordinatenmesstechnik anwendbar (Abb. 36). Wegen der kurzen Messzeiten bei Objekten mit vielen Merkmalen führt die Anwendung dieser Geräte zu einer erheblichen Beschleunigung von Prozessketten und zur Erhöhung der Wirtschaftlichkeit.

<p>Abb. 36: TomoScope® S: die aktuelle Version des 2005 vorgestellten ersten Koordinatenmessgeräts mit Röntgentomografie – optional mit Multisensorik</p>

Röntgenstrahlung durchdringt das Messobjekt

Für die Röntgentomografie wird die Fähigkeit der Röntgenstrahlung genutzt, Objekte zu durchdringen. Auf dem Weg durch ein Objekt wird ein Teil der auftreffenden Strahlung absorbiert. Je länger die Durchstrahlungslänge im Objekt ist, desto weniger Strahlung tritt hinter dem Objekt wieder aus. Darüber hinaus hängt die Absorption aber auch vom Material ab. Ein Röntgendetektor erfasst die auftreffende Röntgenstrahlung als zweidimensionales Durchstrahlungsbild. Bei Seitenlängen der Detektoren von ca. 50 mm bis 400 mm kann ein großer Teil der Messobjekte jeweils in einem Bild erfasst werden.

Durchstrahlungsbilder, Voxel-Volumen und Punktewolken

Um ein Objekt zu tomografieren, werden nacheinander einige hundert solcher zweidimensionalen Durchstrahlungsbilder in verschiedenen Drehlagen des Messobjekts aufgenommen (Abb. 37a). Das Objekt befindet sich dazu auf einem Drehtisch, der sukzessive weitergedreht wird. Die in dieser Bildfolge enthaltene dreidimensionale Information über das Messobjekt wird durch geeignete mathematische Verfahren (Rückprojektion) extrahiert und als so genanntes Voxel-Volumen, bestehend aus vielen Einzelvoxeln zur Verfügung gestellt. Jedes Voxel (von Volumen und Pixel) verkörpert für einen definierten Ort im Messvolumen die Absorptionseigenschaften des Messobjekts bzw. der umgebenden Luft. Ähnlich wie bei der zweidimensionalen Bildverarbeitung werden aus den Voxel-Daten mit geeigneten Schwellwert- oder anderen Verfahren die eigentlichen Messpunkte berechnet. Dies kann mit einer Auflösung und Genauigkeit bis auf Bruchteile der Voxelgröße realisiert werden (»Subvoxeling«, [7]).

Die eingesetzten Sensoren weisen gegenwärtig bis zu 16 Millionen Bildpunkte auf. Im Messvolumen ergeben sich hieraus typischerweise einige Hunderttausend bis wenige Millionen Messpunkte, die gleichmäßig über die Oberfläche des zu messenden Teils verteilt sind. Es werden auch Geometrien im Inneren der Messobjekte wie Hohlräume oder Hinterschnitte erfasst. Die Messpunkte können mit den bekannten Methoden der Koordinatenmesstechnik ausgewertet werden.

Durchstrahlungsbilder, Voxel-Volumen und Punktewolken
<p>Abb. 37: Röntgentomografie: Die von einer punktförmigen Röntgenquelle ausgehende Strahlung gelangt durch das Messobjekt auf den Flächensensor. Es werden Bilder in verschiedenen Drehlagen aufgenommen. a) geringe Vergrößerung, b) höhere Vergrößerung, c) Rastertomografie</p>

Rastertomografie

Ähnlich wie bei der Messung mit einer Bildverarbeitung ist es bei der Tomografie möglich, die Vergrößerung zu verändern, um kleine Teile mit hoher Vergrößerung oder größere Teile komplett mit geringerer Vergrößerung zu erfassen (Abb. 37b). Hierzu werden entweder das Messobjekt innerhalb des Strahlengangs oder die Röntgenkomponenten (Röntgenquelle und Detektor) relativ zum Messobjekt in axialer Richtung verschoben. In manchen Fällen reicht die Größe des Sensors oder die zur Verfügung stehende Pixelanzahl dennoch nicht aus, um große Teile oder kleine Merkmale mit ausreichender Auflösung zu tomografieren. In solchen Fällen werden der Drehtisch mit dem Messobjekt und die Röntgenkomponenten relativ zueinander verschoben. Anschließend werden die so aufgenommenen Bilder bzw. Volumenabschnitte exakt aneinandergefügt (Rastertomografie, Abb. 37c).

Vielfältige Anwendungen

Die Anwendungsmöglichkeiten der Röntgentomografie sind praktisch nur durch die Durchstrahlbarkeit der zu messenden Objekte und die Genauigkeitsanforderungen begrenzt. Die weiteste Verbreitung hat diese Technik deshalb beim Kunststoffspritzen gefunden. Neben der schnellen Erstbemusterung vieler Merkmale können die herstellungsbedingten Abweichungen gegenüber dem CAD-Modell erfasst werden.

Werkzeugkorrektur automatisiert

Das Modell für das Werkzeug wird nachfolgend über entsprechende Softwarefunktionen automatisch oder manuell gezielt verändert. So werden korrigierte Werkzeuge hergestellt und Verfahrenseinflüsse kompensiert. Praktische Anwendungen sind das Messen von Autoscheinwerfern, Steckermodulen, Schneidkanten von Scherköpfen für Elektrorasierer und der Gesamtgeometrie von Dieseleinspritzdüsen. Das Verfahren kann auch zur Prüfung der Maße von Komponenten montierter Baugruppen und innenliegender Geometrien sowie zur Werkstoffanalyse (Einschlüsse) eingesetzt werden.

Die Röntgentomografie hat sich innerhalb der Koordinatenmesstechnik zu einem eigenständigen Fachgebiet entwickelt. Physikalische Hintergründe, weitere Messverfahren, Anwendungsgebiete und das Thema »Genauigkeit« werden in Band 331 der Reihe Die Bibliothek der Technik [8] ausführlicher dargestellt.

Werth Computertomografie CT

Koordinatemesssystem mit Computertomografie